Mis cursos en CIMAT
- Otoño 2020Teoría de números algebraicos
- Otoño 2019Funciones zeta aritméticas
Mis cursos en San Salvador
- Agosto 2019Teoría de esquemas
- Primavera de 2019Bases de Gröbner
- Primavera de 2019Álgebra I
- 2018Álgebra conmutativa
- Junio de 2018Categorías
- Abril de 2018Números p-ádicos
- 2018Álgebra I y II
- Febrero de 2017Números de Bernoulli
- Agosto de 2016Álgebra homológica
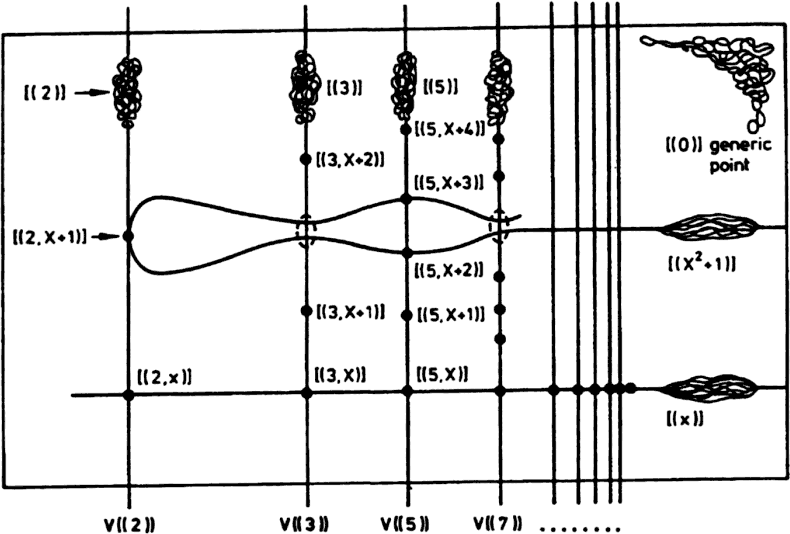
Este seminario está dedicado a los esquemas que generalizan las variedades algebraicas. Las fuentes sugeridas son [G-W, Cap. 1-4], [E-H, Cap. I, II, VI], [Man], y [Sha, Cap. 5]. Los prerrequisitos son álgebra conmutativa, topología general y teoría de categorías.
En total habrá solamente 10 sesiones, que apenas bastan para explicar qué es un esquema, así que se trata de una invitación a la teoría de esquemas.
Apuntes
Invitación a la teoría de esquemas (actualizados el 29 de agosto de 2019)
Cronograma
- Sesión 1 (12/08/19). Definimos el espacio $\operatorname{Spec} A$ e investigamos sus propiedades topológicas.
- Sesión 2 (13/08/19). Definimos prehaces, haces, fibras y hacificación.
- Sesión 3 (14/08/19). Terminamos nuestra introducción a la teoría de haces por la imagen directa $f_*\mathcal{F}$ e inversa $f^{-1}\mathcal{G}$ y la adjunción $\operatorname{Hom}_X (f^{-1} \mathcal{G}, \mathcal{F}) \cong \operatorname{Hom}_Y (\mathcal{G}, f_* \mathcal{F})$. Definimos espacios anillados y localmente anillados $(X,\mathcal{O}_X)$ y sus morfismos.
- Sesión 4 (15/08/19). Definimos la estructura de espacio localmente anillado $(\operatorname{Spec} A, \mathcal{O}_{\operatorname{Spec} A})$ y los esquemas afines como espacios localmente anillados $(X,\mathcal{O}_X) \cong (\operatorname{Spec} A, \mathcal{O}_{\operatorname{Spec} A})$. Probamos que la categoría de esquemas afines es (anti)equvalente a la categoría de anillos conmutativos.
- Sesión 5 (19/08/19). Al inicio de clase volvimos a la construcción del haz estructural de $\operatorname{Spec} A$ para describirlo en el caso particular cuando $A$ es un dominio. Luego probamos un resultado más general que la antiequivalencia de la vez pasada: si $(X, \mathcal{O}_X)$ es cualquier espacio localmente anillado e $(Y, \mathcal{O}_Y)$ es un esquema afín, entonces las secciones globales nos dan una biyección $\operatorname{Hom}_\mathbf{ELA} (X,Y) \cong \operatorname{Hom}_\mathbf{Anillos} (\mathcal{O}_Y (Y), \mathcal{O}_X (X))$. Terminamos por la noción del subesquema cerrado $V (\mathfrak{a}) \subseteq \operatorname{Spec} A$ asociado a un ideal $\mathfrak{a} \subseteq A$.
- Sesión 6 (20/08/19). Introdujimos esquemas en general. Como un ejemplo de esquema no afín, tomamos el plano sin origen $\mathbb{A}^2_k\setminus\{0\}$. Terminamos por la definición de $S$-esquemas.
- Sesión 7 (21/08/19). Hablamos del pegamiento de haces y sus morfismos.
- Sesión 8 (22/08/19). Hablamos del pegamiento de espacios localmente anillados (y en particular de esquemas) y sus morfismos.
- Sesión 9 (26/08/19). Construimos los productos fibrados de esquemas $X\times_S Y$.
- Sesión 10 (27/08/19). Hablamos del funtor de puntos $R\text{-}\mathbf{Alg} \to \mathbf{Set}$ que determina un esquema $X$ sobre $R$.
Referencias
- [G-W] Ulrich Görtz, Torsten Wedhorn, Algebraic Geometry I: Schemes
- [E-H] David Eisenbud, Joe Harris, The Geometry of Schemes
- [Man] Yu.I. Manin, Introduction to the Theory of Schemes
- [Sha] I.R. Shafarevich, Basic Algebraic Geometry 2: Schemes and Complex Manifolds
Contacto
No duden en contactarme por cualquier pregunta sobre el curso: cadadr@gmail.com.